How we equip our users to unlock the full potential of H-Series Quantum Computers

In our latest paper, we’ve taken a big step toward large scale fault-tolerant quantum computing, squeezing up to 94 error-detected qubits (and 48 error-corrected qubits) out of just 98 physical qubits, a low-fat encoding that cuts overhead to the bone. With 64 of our logical qubits, we were able to simulate quantum magnetism at a scale that can be exceedingly difficult for classical computers.

The "holy grail" of quantum computing is universal fault-tolerance: the ability to correct errors faster than they occur during any computation. To realize this, we aim to create “logical qubits,” which are groups of entangled physical qubits that share quantum information in a way that protects it. Better protection leads to lower “logical” error rate and greater ability to solve complex problems.

However, it’s never that easy. An unofficial law of physics is “there’s no such thing as a free lunch”. Creating high quality, low error-rate logical qubits often costs many physical qubits, thus reducing the size of calculations you can run, despite your new, lower-than-ever error rates.

With our latest paper, we are thrilled to announce that we have hit a key milestone on the Quantinuum roadmap: an ultra-efficient method for creating logical qubits, extracting a whopping 48 error-corrected and 64 error-detected logical qubits out of just 98 physical qubits. Our logical qubits boasted better than “break-even” fidelity, beating their physical counterparts with lower error rates on several different fronts. And still that isn’t the end of the story: we used our 64 error-detected logical qubits in a large-scale quantum magnetism simulation, laying the groundwork for future studies of exotic interactions in materials.

Stacking Wins

To get this world-leading result, we employed a neat trick: ‘nesting’ super efficient quantum error-detecting codes together to make a new, ultra-efficient error-correcting code. Dr. DeCross, a primary author on the paper, said this nesting is like “braiding together ropes made out of ropes made out of ropes”.  Physicists call this ‘code concatenation’, and you can think of it as adding layers of protection on top of each other.

To begin, we took the now-famous ‘iceberg code’, a quantum error detection code that gives an almost 1:1 ratio of physical qubits to logical qubits. The iceberg code only detects errors, however, which means that instead of actually correcting errors it lets you throw out bits where errors were detected. To make a code that could both detect and correct errors, we concatenated two iceberg codes together, giving a code that can correct small errors while still boasting a world-record 2:1 physical:logical ratio (physicists call this a “high encoding rate”).

The team then benchmarked the logical qubits, checking large system-scale operations and comparing them to their physical counterparts. This introduces a crucial hurdle to clear: oftentimes, researchers end up with logical qubits that perform *worse* than their physical counterparts. It’s critical that logical qubits actually beat physical ones, after all – that is the whole point!

Thanks to some clever circuit design and our natively high fidelities, the new logical qubits outperformed their physical counterparts in every test we performed, sometimes by a factor of 10 to 100.

Computing Logically

Of course, the whole point is to use our logical qubits for something useful, the ultimate measure of functionality. With 64 error-detected qubits, we performed a simulation of quantum magnetism; a crucial milestone that validates our roadmap.

The team took extra care to perform their simulation in 3 dimensions to best reflect the real-world (often, studies like this will only be in 1D or 2D to make them easier). Problems like this are both incredibly important for expanding our understanding of materials, but are also incredibly hard, as their complexity scales quickly. To make qubits interact as if they are in a 3D material when they are trapped in 2D inside the computer, we used our all-to-all connectivity, a feature that results from our movable qubits.

Maximizing Entanglement

Breaking the encoding rate record and performing a world-leading logical simulation wasn’t enough for the team. For their final feat, the team generated 94 error-detected logical qubits, and entangled them all in a special state called a “GHZ” state (also known as a ‘cat’ state, alluding to Schrödinger’s cat). GHZ states are often used by experts as a simple benchmark for showcasing quantum computing’s unique capacity to use entanglement across many qubits. Our best 94-logical qubit GHZ state boasted a fidelity of 94.9%, crushing its un-encoded counterpart.

Logical Qubits Are the New Normal

Taken together, these results show that we can suppress errors more effectively than ever before, proving that Helios is capable of delivering complex, high-fidelity operations that were previously thought to be years away. While the magnetism simulation was only error-detected, it showcases our ability to protect universal computations with partially fault-tolerant methods. On top of that, the team also demonstrated key error-corrected primitives on Helios at scale.

All of this has real-world implications for the quantum ecosystem: we are working to package these iceberg codes into QCorrect, an upcoming tool that will help developers automatically improve the performance of their own applications.

This is just the beginning: we are officially entering the era of large-scale logical computing. The path to fault-tolerance is no longer just theoretical—it is being built, gate by gate, on Helios.

Japan has made bold, strategic investments in both high-performance computing (HPC) and quantum technologies. As these capabilities mature, an important question arises for policymakers and research leaders: how do we move from building advanced machines to demonstrating meaningful, integrated use?

Last year, Quantinuum installed its Reimei quantum computer at a world-class facility in Japan operated by RIKEN, the country’s largest comprehensive research institution. The system was integrated with Japan’s famed supercomputer Fugaku, one of the most powerful in the world, as part of an ambitious national project commissioned by the New Energy and Industrial Technology Development Organization (NEDO), the national research and development entity under the Ministry of Economy, Trade and Industry.

Now, for the first time, a full scientific workflow has been executed across Fugaku, one of the world’s most powerful supercomputers, and Reimei, our trapped-ion quantum computer. This marks a transition from infrastructure development to practical deployment.

Quantum Biology

In this first foray into hybrid HPC-quantum computation, the team explored chemical reactions that occur inside biomolecules such as proteins. Reactions of this type are found throughout biology, from enzyme functions to drug interactions.

Simulating such reactions accurately is extremely challenging. The region where the chemical reaction occurs—the “active site”—requires very high precision, because subtle electronic effects determine the outcome. At the same time, this active site is embedded within a much larger molecular environment that must also be represented, though typically at a lower level of detail.

To address this complexity, computational chemistry has long relied on layered approaches, in which different parts of a system are treated with different methods. In our work, we extended this concept into the hybrid computing era by combining classical supercomputing with quantum computing.

Shifting the Paradigm

While the long-term goal of quantum computing is to outperform classical approaches alone, the purpose of this project was to demonstrate a fully functional hybrid system working as an end-to-end platform for real scientific applications. We believe it is not enough to develop hardware in isolation – we must also build workflows where classical and quantum resources create a whole that is greater than the parts. We believe this is a crucial step for our industry; large-scale national investments in quantum computing must ultimately show how the technology can be embedded within existing research infrastructure.

In this work, the supercomputer Fugaku handled geometry optimization and baseline electronic structure calculations. The quantum computer Reimei was used to enhance the treatment of the most difficult electronic interactions in the active site, those that are known to challenge conventional approximate methods. The entire process was coordinated through Quantinuum’s workflow system Tierkreis, which allows jobs to move efficiently between machines.

Hybrid Computation is Now an Operational Reality

With this infrastructure in place, we are now poised to truly leverage the power of quantum computing. In this instance, the researchers designed the algorithm to specifically exploit the strengths of both the quantum and the classical hardware.

First, the classical computer constructs an approximate description of the molecular system. Then, the quantum computer is used to model the detailed quantum mechanics that the classical computer can’t handle. Together, this improves accuracy, extending the utility of the classical system.

A Path to Hybrid Advantage

Accurate simulation of biomolecular reactions remains one of the major challenges in biochemistry. Although the present study uses simplified systems to focus on methodology, it lays the groundwork for future applications in drug design, enzyme engineering, and photoactive biological systems.

While fully fault-tolerant, large-scale quantum computers are still under development, hybrid approaches allow today’s quantum hardware to augment powerful classical systems, such as Fugaku, to explore meaningful applications. As quantum technology matures, the same workflows can scale accordingly.

High-performance computing centers worldwide are actively exploring how quantum devices might integrate into their ecosystems. By demonstrating coordinated job scheduling, direct hardware access, and workflow orchestration across heterogeneous architectures, this work offers a concrete example of how such integration can be achieved.

As quantum hardware matures, we believe the algorithms and workflows developed here can be extended to increasingly realistic and industrially relevant problems. For Japan’s research ecosystem, this first application milestone signals that hybrid quantum–supercomputing is moving from ambition to implementation.

Authors: 
Quantinuum (alphabetical order): Eric Brunner, Steve Clark, Fabian Finger, Gabriel Greene-Diniz, Pranav Kalidindi, Alexander Koziell-Pipe, David Zsolt Manrique, Konstantinos Meichanetzidis, Frederic Rapp
Hiverge (alphabetical order): Alhussein Fawzi, Hamza Fawzi, Kerry He, Bernardino Romera Paredes, Kante Yin

‍

What if every quantum computing researcher had an army of students to help them write efficient quantum algorithms? Large Language Models are starting to serve as such a resource.

Quantinuum’s processors offer world-leading fidelity, and recent experiments show that they have surpassed the limits of classical simulation for certain computational tasks, such as simulating materials. However, access to quantum processors is limited and can be costly. It is therefore of paramount importance to optimise quantum resources and write efficient quantum software. Designing efficient algorithms is a challenging task, especially for quantum algorithms: dealing with superpositions, entanglement, and interference can be counterintuitive.

To this end, our joint team used Hiverge’s AI platform for automated algorithm discovery, the Hive, to probe the limits of what can be done in quantum chemistry. The Hive generates optimised algorithms tailored to a given problem, expressed in a familiar programming language, like Python. Thus, the Hive’s outputs allow for increased interpretability, enabling domain experts to potentially learn novel techniques from the AI-discovered solutions. Such AI-assisted workflows lower the barrier of entry for non-domain experts, as an initial sketch of an algorithmic idea suffices to achieve state-of-the-art solutions.

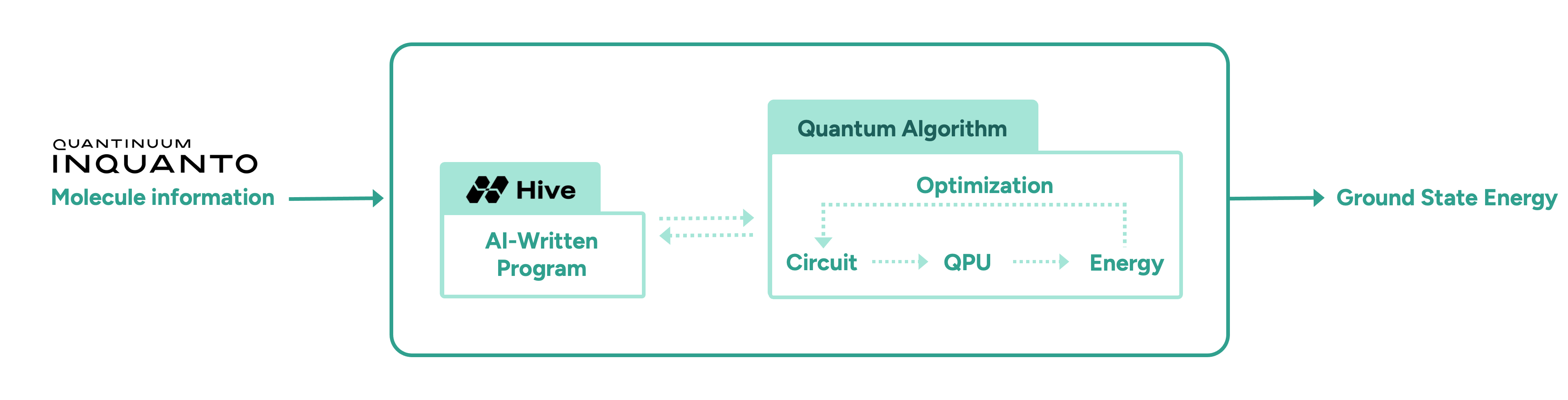
In this initial proof-of-concept study, we demonstrate the advantage of AI-driven algorithmic discovery of efficient quantum heuristics in the context of quantum chemistry, in particular the electronic structure problem. Our early explorations show that the Hive can start from a naïve and simple problem statement and evolve a highly optimised quantum algorithm that solves the problem, reaching chemical precision for a collection of molecules. Our high-level workflow is shown in Figure 1. Specifically, the quantum algorithm generated by the Hive achieves a reduction in the quantum resources required by orders of magnitude compared to current state-of-the-art quantum algorithms. This promising result may enable the implementation of quantum algorithms on near-term hardware that was previously thought impossible due to current resource constraints.

The Electronic Structure Problem in Quantum Chemistry

The electronic structure problem is central to quantum chemistry. The goal is to prepare the ground state (the lowest energy state) of a molecule and compute the corresponding energy of that state to chemical precision or beyond. Classically, this is an exponentially hard problem. In particular, classical treatments tend to fall short when there are strong quantum effects in the molecule, and this is where quantum computers may be advantageous.

The paradigm of variational quantum algorithms is motivated by near-term quantum hardware. One starts with a relatively easy-to-prepare initial state. Then, the main part of the algorithm consists of a sequence of parameterised operators representing chemically meaningful actions, such as manipulating electron occupations in the molecular orbitals. These are implemented in terms of parameterised quantum gates. Finally, the energy of the state is measured via the molecule’s energy operator, the “Hamiltonian”, by executing the circuit on a quantum computer and measuring all the qubits on which the circuit is implemented. Taking many measurements, or “shots”, the energy is estimated to the desired precision. The ground state energy is found by iteratively optimising the parameters of the quantum circuit until the energy converges to a minimum value. The general form of such a variational quantum algorithm is illustrated in Figure 2.

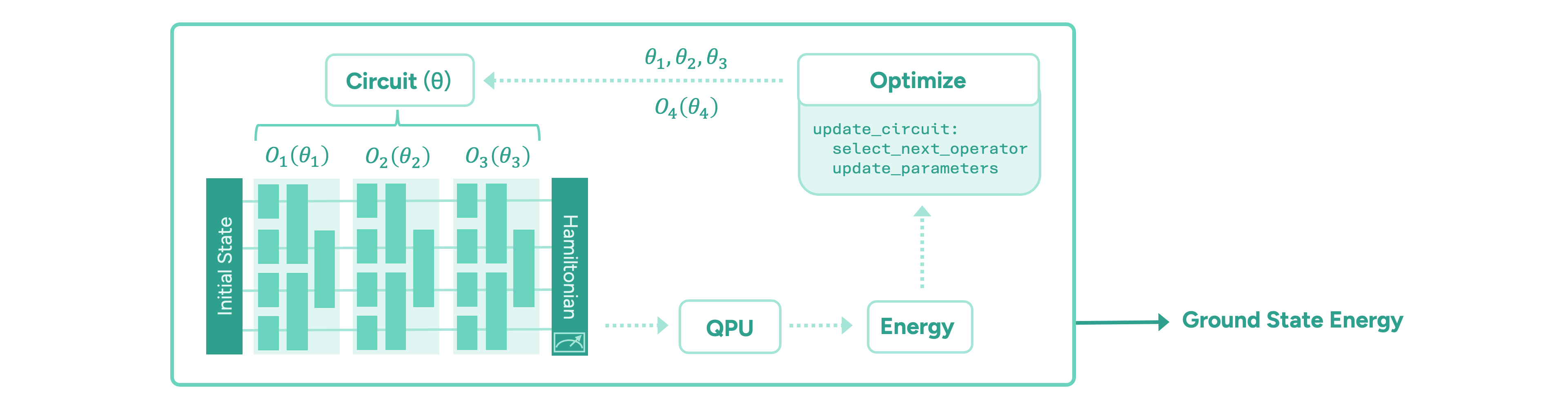
The main challenge in these frameworks is to design an appropriate quantum circuit architecture, i.e. find an efficient sequence of operators, and an efficient optimisation strategy for its parameters. It is important to minimise the number of quantum operations in any given circuit, as each operation is inherently noisy and the algorithm’s output degrades exponentially. Another important quantum resource to be minimised is the total number of circuits that need to be evaluated to compute the energy values during the optimisation of the circuit parameters, which is time-consuming.

To meet these challenges, we task the Hive with designing a variational quantum algorithm to solve the ground state problem, following the workflow shown in Figure 1. The Hive is a distributed evolutionary process that evolves programs. It uses Large Language Models to generate mutations in the form of edits to an entire codebase. This genetic process selects the fittest programs according to how well they solve a given problem. In our case, the role of the quantum computer is to compute the fitness, i.e., the ground state energy. Importantly, the Hive operates at the level of a programming language; it readily imports and uses all known libraries that a human researcher would use, including Quantinuum’s quantum chemistry platform, InQuanto. In addition, the Hive can accept instructions and requests in natural language, increasing its flexibility. For example, we encouraged it to seek parameter optimisation strategies that avoid estimating gradients, as this incurs significant overhead in terms of circuit evaluations.  Intuitively, the interaction between a human scientist and the Hive is analogous to a supervisor and a group of eager and capable students: the supervisor provides guidance at a high level, and the students collaborate and flesh out the general idea to produce a working solution that the supervisor can then inspect.

We find that from an extremely basic starting point, consisting of a skeleton for a variational quantum algorithm, the Hive can autonomously assemble a bespoke variational quantum algorithm, which we call Hive-ADAPT. Specifically, the Hive evolves heuristic functions that construct a circuit as a sequence of quantum operators and optimise its parameters. Remarkably, the Hive converged on a structure resembling the current state-of-the-art, ADAPT-VQE. Crucially, however, Hive-ADAPT substantially outperforms this baseline, delivering significant improvements in chemical precision while reducing quantum resource requirements.

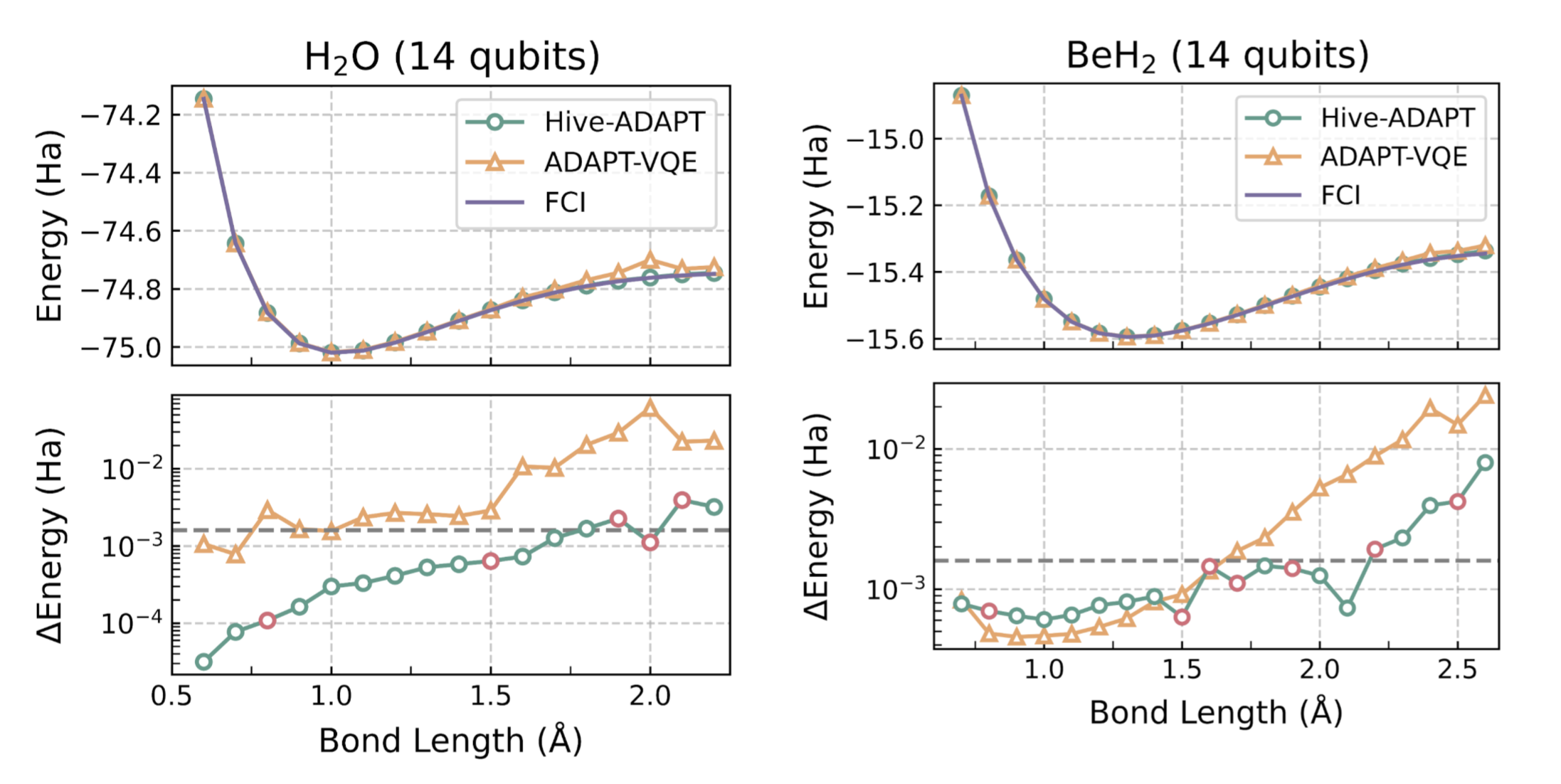
A molecule’s ground state energy varies with the distances between its atoms, called the “bond length”. For example, for the molecule H2O, the bond length refers to the length of the O-H bond. The Hive was tasked with developing an algorithm for a small set of bond lengths and reaching chemical precision, defined as within 1.6e-3 Hartree (Ha) of the ground state energy computed with the exact Full Configuration Interaction (FCI) algorithm. As we show in Figure 3, remarkably, Hive-ADAPT achieves chemical precision for more bond lengths than ADAPT-VQE. Furthermore, Hive-ADAPT also reaches chemical precision for other “unseen” bond lengths, showcasing the generalisation ability of the evolved quantum algorithm. Our results were obtained from classical simulations of the quantum algorithms, where we used NVIDIA CUDA-Q to leverage the parallelism enabled by GPUs. Further, relative to ADAPT-VQE, Hive-ADAPT exhibits one to two orders of magnitude reduction in quantum resources, such as the number of circuit evaluations and the number of operators used to construct circuits, which is crucial for practical implementations on actual near-term processors.

For molecules such as BeH2 at large Be-H bond lengths, a complex initial state is required for the algorithm to be able to reach the ground state using the available operators. Even in these cases, by leveraging an efficient state preparation scheme implemented in InQuanto, the Hive evolved a dedicated strategy for the preparation of such a complex initial state, given a set of basic operators to achieve the desired chemical precision.

To validate Hive-ADAPT under realistic conditions, we employed Quantinuum’s H2 Emulator, which provides a faithful classical simulator of the H2 quantum computer, characterised by a 1.05e-3 two-qubit gate error rate. Leveraging the Hive's inherent flexibility, we adapted the optimisation strategy to explicitly penalise the number of two-qubit gates—the dominant noise source on near-term hardware—by redefining the fitness function. This constraint guided the Hive to discover a noise-aware algorithm capable of constructing hardware-efficient circuits. We subsequently executed the specific circuit generated by this algorithm for the LiH molecule at a bond length of 1.5 Å with the Partition Measurement Symmetry Verification (PMSV) error mitigation procedure. The resulting energy of -7.8767 ± 0.0031 Ha, obtained using 10,000 shots per circuit with a discard rate below 10% in the PMSV error mitigation procedure, is close to the target FCI energy of -7.8824 Ha and demonstrates the Hive's ability to successfully tailor algorithms that balance theoretical accuracy with the rigorous constraints of hardware noise and approach chemical precision as much as possible with current quantum technology.

For illustration purposes, we show an example of an elaborate code snippet evolved by the Hive starting from a trivial version:

Quantinuum’s in-house quantum chemistry expert, Dr. David Zsolt Manrique, commented,

“I found it amazing that the Hive converged to a domain-expert level idea. By inspecting the code, we see it has identified the well-known perturbative method, ‘MP2’, as a useful guide; not only for setting the initial circuit parameters, but also for ordering excitations efficiently. Further, it systematically and laboriously fine-tuned those MP2-inspired heuristics over many iterations in a way that would be difficult for a human expert to do by hand. It demonstrated an impressive combination of domain expertise and automated machinery that would be useful in exploring novel quantum chemistry methods.”

Looking to the Future

In this initial proof-of-concept collaborative study between Quantinuum and Hiverge, we demonstrate that AI-driven algorithm discovery can generate efficient quantum heuristics. Specifically, we found a great reduction in quantum resources, which is impactful for quantum algorithmic primitives that are frequently reused. Importantly, this approach is highly flexible; it can accommodate the optimisation of any desired quantum resource, from circuit evaluations to the number of operations in a given circuit. This work opens a path toward fully automated pipelines capable of developing problem-specific quantum algorithms optimised for NISQ as well as future hardware.

An important question for further investigation regards transferability and generalisation of a discovered quantum solution to other molecules, going beyond the generalisation over bond lengths of the same molecule that we have already observed. Evidently, this approach can be applied to improving any other near-term quantum algorithm for a range of applications from optimisation to quantum simulation.

We have already demonstrated an error-corrected implementation of quantum phase estimation on quantum hardware, and an AI-driven approach promises further hardware-tailored improvements and optimal use of quantum resources. Beyond NISQ, we envision that AI-assisted algorithm discovery will be a fruitful endeavour in the fault-tolerant regime, as well, where high-level quantum algorithmic primitives (quantum fourier transform, amplitude amplification, quantum signal processing, etc.) are to be combined optimally to achieve computational advantage for certain problems.

Notably, we’ve entered an era where quantum algorithms can be written in high-level programming languages, like Quantinuum’s Guppy, and approaches that integrate Large Language Models directly benefit. Automated algorithm discovery is promising for improving routines relevant to the full quantum stack, for example, in low-level quantum control or in quantum error correction.